Algebra II: Linear and Quadratic Functions
Algebra II: Linear Functions
*Note: This section covers key concepts related to linear functions.*
Forms of Linear Equations
- Slope-Intercept Form: y = mx + b, where ‘m’ represents the slope (steepness of the line), ‘b’ is the y-intercept (where the line crosses the y-axis), ‘x’ is the independent variable, and ‘y’ is the dependent variable.
- Point-Slope Form: y – y₁ = m(x – x₁), where ‘m’ is the slope, and (x₁, y₁) is a given point on the line. ‘x’ and ‘y’ remain as variables.
- Standard Form: Ax + By = C, where ‘A’, ‘B’, and ‘C’ are constants, and ‘x’ and ‘y’ are variables.
Converting Between Forms
From Point-Slope to Slope-Intercept:
Example: y – 8 = (2/4)(x – 4)
- y = (2/4)(x – 4) + 8
- y = (2/4)x – 2 + 8
- y = (2/4)x + 6
From Standard to Slope-Intercept:
Example: 10x + 5y = 30
- 5y = -10x + 30
- y = -2x + 6
Parallel and Perpendicular Lines
- Parallel Lines: Parallel lines have the same slope.
- Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other.
Horizontal and Vertical Lines
- Horizontal Line: A horizontal line has the equation y = c, where ‘c’ is a constant.
- Vertical Line: A vertical line has the equation x = c, where ‘c’ is a constant.
Graphing Linear Inequalities
To graph an inequality, first graph the corresponding equation as a line. Use a dashed line for < or >, and a solid line for ≤ or ≥. Then, shade the region that satisfies the inequality. Use a test point (usually (0, 0)) to determine which side of the line to shade.
Algebra II: Quadratic Functions
*Note: This section covers key concepts related to quadratic functions.*
Intercepts
- X-Intercept: The x-intercept is found when y = 0. You can use the quadratic formula to solve for ‘x’ when y = 0.
- Y-Intercept: The y-intercept is found when x = 0. Substitute x = 0 into the equation and solve for ‘y’.
Function Notation
Function notation, f(x), replaces ‘y’ in an equation. For example, f(x) = 2x – 5. If f(5) is given, then x = 5, and you must solve for ‘y’. If f(x) = 5, then y = 5, and you must solve for ‘x’.
Domain and Range
The domain of a function is the set of all possible x-values. The range is the set of all possible y-values.

In the image above, the domain is all real numbers, or (-∞, ∞), because the graph extends infinitely in both directions along the x-axis. The range is also all real numbers, or (-∞, ∞), because the graph extends infinitely in both directions along the y-axis. A bracket indicates that a point is included, while a parenthesis indicates that a point is not included.
Forms of Quadratic Equations
- Standard Form: ax² + bx + c = 0, where ‘a’ is the coefficient of x², ‘b’ is the coefficient of x, and ‘c’ is the constant.
- Vertex Form:
- For a parabola (U-shape): y = a(x – h)² + k
- For an absolute value (V-shape): f(x) = a|x – h| + k
In vertex form, ‘a’ determines the vertical stretch, ‘h’ determines the horizontal shift, and ‘k’ determines the vertical shift.
Converting Standard Form to Vertex Form
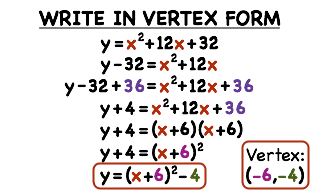
Quadratic Formula
The quadratic formula, x = [-b ± √(b² – 4ac)] / 2a, is used to find the solutions (roots) of a quadratic equation in the form ax² + bx + c = 0. Substitute the values of ‘a’, ‘b’, and ‘c’ from the equation into the formula to solve for ‘x’.

