NFA, DFA, Automata, Parsing, and Regular Expressions

Posted on Feb 18, 2025 in Commerce

NFA vs. DFA

Here’s a comparison of NFA (Non-deterministic Finite Automaton) and DFA (Deterministic Finite Automaton):

NFA: The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic.
DFA: The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic.
NFA: Permits empty string transitions.
DFA: Empty string transitions are not seen in DFA.
NFA: Backtracking is not always possible.
DFA: Backtracking is allowed.
NFA: Requires less space.
DFA: Requires more space.
NFA: A string is accepted if at least one of all possible transitions ends in a final state.
DFA: A string is accepted if it transits to a final state.

Myhill-Nerode Theorem

The Myhill-Nerode Theorem is a fundamental concept in automata theory. Here’s a simplified explanation:

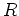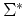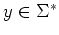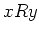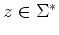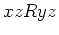An equivalence relation $R$ on $\Sigma^{*}$ is said to be right invariant if for every $x$ , $y \in \Sigma^{*}$ , if $x R y$ then for every $z \in \Sigma^{*}$ , $xz R yz$ .

An equivalence relation is of finite index if the set of its equivalence classes is finite.

The Myhill-Nerode Theorem states the following three statements are equivalent:

A language 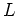is regular.
L is the union of some of the equivalence classes of a right invariant equivalent relation of finite index.
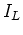$I_{L}$ is of finite index.

Parsing

Q2. What do you mean by Parsing?

Parsing is the process of deriving a string using the production rules of a grammar. It checks the acceptability of a string and determines if it’s syntactically correct. A parser takes inputs and builds a parse tree.

There are two main types of parsers:

Top-Down Parser: Starts from the top with the start symbol and derives a string using a parse tree.
Bottom-Up Parser: Starts from the bottom with the string and works up to the start symbol using a parse tree.

Design of Top-Down Parsers

For top-down parsing, a PDA (Pushdown Automaton) has these transitions:

Pop the non-terminal on the left-hand side of the production at the top of the stack and push its right-hand side string.
If the top symbol of the stack matches the input symbol being read, pop it.
Push the start symbol S into the stack.
If the input string is fully read and the stack is empty, go to the final state F.

Example: Design a top-down parser for the expression “x+y*z” for the grammar G with the following production rules: P: S ¨ S+X | X, X ¨ X*Y | Y, Y ¨ (S) | id

Design of Bottom-Up Parsers

For bottom-up parsing, a PDA has these transitions:

Push the current input symbol into the stack.
Replace the right-hand side of a production at the top of the stack with its left-hand side.
If the top of the stack element matches the current input symbol, pop it.
If the input string is fully read and only the start symbol S remains in the stack, pop it and go to the final state F.

Example: Design a bottom-up parser for the expression “x+y*z” for the grammar G with the following production rules: P: S ¨ S+X | X, X ¨ X*Y | Y, Y ¨ (S) | id

Pushdown Automaton (PDA)

A pushdown automaton (PDA) is a way to implement a context-free grammar, similar to how we design a DFA for a regular grammar. A DFA has finite memory, but a PDA can have infinite memory.

A PDA is essentially a “Finite state machine” + “a stack”.

A PDA has three components:

An input tape
A control unit
A stack with infinite size

The stack head scans the top symbol of the stack.

A stack has two operations:

Push: A new symbol is added at the top.
Pop: The top symbol is read and removed.

A PDA may or may not read an input symbol, but it *must* read the top of the stack in every transition.

A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q₀, I, F):

Q: The finite number of states.
∑: Input alphabet.
S: Stack symbols.
δ: The transition function: Q × (∑ ∪ {ε}) × S × Q × S*.
q₀: The initial state (q₀ ∈ Q).
I: The initial stack top symbol (I ∈ S).
F: A set of accepting states (F ∈ Q).

The following diagram shows a transition in a PDA from a state q₁ to state q₂, labeled as a,b → c:

This means at state q₁, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack, and move to state q₂.

Regular Sets

Q4. Regular Set (Discuss)

A regular set is any set that represents the value of a regular expression.

Properties of Regular Sets:

Property 1: The union of two regular sets is regular.
Property 2: The intersection of two regular sets is regular.
Property 3: The complement of a regular set is regular.
Property 4: The difference of two regular sets is regular.
Property 5: The reversal of a regular set is regular.
Property 6: The closure of a regular set is regular.
Property 7: The concatenation of two regular sets is regular.

Identities Related to Regular Expressions

Given R, P, L, and Q as regular expressions, the following identities hold:

?* = å
å* = å
RR* = R*R
R*R* = R*
(R*)* = R*
RR* = R*R
(PQ)*P = P(QP)*
(a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
R + ? = ? + R = R (The identity for union)
R å = å R = R (The identity for concatenation)
? L = L ? = ? (The annihilator for concatenation)
R + R = R (Idempotent law)
L (M + N) = LM + LN (Left distributive law)
(M + N) L = LM + LN (Right distributive law)
å + RR* = å + R*R = R*

chapter08.doc.anc28

Pumping Lemma

The Pumping Lemma describes an essential property of all regular languages.

Theorem

Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L:

|w| ≥ c

We can break w into three strings, w = xyz, such that:

|y| > 0
|xy| ≤ c
For all k ≥ 0, the string xy^kz is also in L.

Applications of Pumping Lemma

The Pumping Lemma is used to prove that certain languages are *not* regular. It should *never* be used to show a language *is* regular.

If L is regular, it satisfies the Pumping Lemma.
If L does *not* satisfy the Pumping Lemma, it is non-regular.

Method to Prove a Language L is Not Regular

Assume that L is regular.
The Pumping Lemma should hold for L.
Use the Pumping Lemma to obtain a contradiction:
- Select w such that |w| ≥ c.
- Select y such that |y| ≥ 1.
- Select x such that |xy| ≤ c.
- Assign the remaining string to z.
- Select k such that the resulting string is not in L.

Therefore, L is not regular.