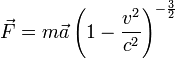Physics: A Comprehensive Exploration of Matter, Energy, and Interactions
Physics (from Lat. Physica, and from the Gr. ????????, ?????? neuter plural) is a science of nature that studies the properties of space, time, matter, and energy, and their interactions.
Physics is not just a theoretical science; it is also an experimental science. Like any science, its conclusions are verifiable by experiment, and its theories can make predictions for future experiments. Given the broad field of study of physics and its historical development in relation to other sciences, it can be considered a fundamental or central science because it encompasses chemistry, biology, and electronics, and explains their phenomena.
In its attempt to accurately and truthfully describe natural phenomena, physics has reached unimaginable limits. Current knowledge ranges from the description of microscopic fundamental particles and the birth of stars in the universe—even with a good chance of knowing what happened in the first moments of the birth of our universe—to name a few achievements.
In its search for the ultimate truth of nature, physics has several branches, which can be grouped into five main theories: classical mechanics describes macroscopic motion; electromagnetism describes electromagnetic phenomena such as light; relativity, by Einstein, describes space-time and gravitational interaction; thermodynamics describes molecular events and the exchange of heat; and finally, quantum mechanics describes the behavior of the atomic world.
Classical Mechanics
Classical mechanics describes the motion of macroscopic bodies at speeds much smaller than the speed of light. There are two types of formulations of this mechanism known as Newtonian mechanics and analytical mechanics.
Newtonian mechanics, as its name implies, is intrinsic to Newton’s precepts. From the three laws formulated by Newton and using differential calculus and integral calculus, it leads to a very accurate approximation of physical phenomena. This formulation is also known as vector mechanics and is due to the several magnitudes that must define its vector in an inertial reference system[7].
Analytical mechanics is an abstract mathematical formulation of mechanics. It allows us to move beyond these privileged reference systems and have more general concepts when used to describe movement using the calculus of variations. There are two equivalent formulations: Lagrangian mechanics, a reformulation of mechanics by Joseph Louis Lagrange based on what is now called the Euler-Lagrange equation (second-order differential equations) and the principle of least action; and Hamiltonian mechanics, a reformulation based on a theoretical mass function called Hamiltonian by William Rowan Hamilton. Ultimately, the two are equivalent.[7]
In classical mechanics, in general, there are three invariant points: time is absolute, nature spontaneously follows the principle of least action, and the conception of a given universe.
Electromagnetism
Electromagnetism describes the interaction of charged particles with electric fields and magnetic fields. It can be divided into electrostatics, the study of interactions between charges at rest; and electrodynamics, the study of interactions between moving charges and radiation. The classical theory of electromagnetism is based on the Lorentz force and Maxwell’s equations.
Electrostatics is the study of phenomena associated with charged bodies at rest. As described by Coulomb’s law, these bodies exert forces on each other. Their behavior can be analyzed in terms of the idea of an electric field surrounding any charged body, such that another charged body placed within the field is subject to a force proportional to the magnitude of the charge and the magnitude of the field at its location. Whether the force is attractive or repulsive depends on the polarity of the charge. Electrostatics has many applications, ranging from the analysis of phenomena such as thunderstorms to the study of the behavior of electron tubes.
Electrodynamics is the study of phenomena associated with charged bodies in motion and varying electric and magnetic fields. Since a moving charge produces a magnetic field, electrodynamics refers to effects such as magnetism, electromagnetic radiation, and electromagnetic induction, including practical applications such as the electric generator and electric motor. This area of electrodynamics, known as classical electrodynamics, was systematically explained by James Clerk Maxwell, and Maxwell’s equations describe the phenomena of this area with great generality. A recent development is quantum electrodynamics, which incorporates the laws of quantum theory to explain the interaction of electromagnetic radiation with matter. Paul Dirac, Heisenberg, and Wolfgang Pauli were pioneers in the formulation of quantum electrodynamics. Relativistic electrodynamics provides some corrections to introduce into the description of the movements of charged particles when their speeds approach the speed of light. It applies to the phenomena involved with particle accelerators and electron tubes operating at high voltages and currents.
Electromagnetism encompasses various real-world phenomena such as light. Light is an electromagnetic field radiating from oscillating, accelerated charged particles. Apart from gravity, most of the forces in everyday experience are the result of electromagnetism.
The principles of electromagnetism find application in various disciplines, such as microwaves, antennas, electrical machinery, communications satellites, bioelectromagnetics, plasmas, nuclear research, fiber optics, interference and electromagnetic compatibility, electromechanical energy conversion, weather (by radar), and remote observation. Electromagnetic devices include transformers, electric relays, radio/TV, telephones, electric motors, transmission lines, waveguides, fiber optics, and lasers.
Relativity
Relativity is the theory formulated principally by Albert Einstein in the early twentieth century. It is divided into two bodies of research: special relativity and general relativity.
In the theory of special relativity, Einstein, Lorentz, Minkowski, and others united the concepts of space and time in a four-dimensional framework called space-time. Special relativity theory was revolutionary for its time. It relegated Newton’s absolute time and introduced concepts such as the invariance of the speed of light, time dilation, length contraction, and mass-energy equivalence. In addition to the formulations of special relativity, the laws of physics are invariant in all inertial reference systems. The mathematical result is an upper limit on the speed of light and the elimination of the causal determinism that physics had before. It should be noted that Newton’s laws of motion are a special case of this theory where the mass travels at very low speeds, does not experience any variation in length, and the transformation into energy and time can be considered absolute.
On the other hand, general relativity studies the gravitational interaction as a deformation in the geometry of spacetime. This theory introduces the concepts of the curvature of spacetime as the cause of gravitational interaction, the equivalence principle (which states that all local observers experience the inertial laws of special relativity invariantly), and the description of particle motion by geodesics. General relativity is not the only theory describing gravitational attraction, but it is the most relevant theory with verifiable data. Previously, gravitational interaction was described mathematically by a distribution of masses, but this theory states that not only does the body perceive this interaction, but also energy, through the curvature of space-time, and that is why we need another mathematical language to describe it: tensor calculus. Many phenomena, such as the bending of light by the action of gravity and the deviation in the orbit of Mercury, are perfectly predicted by this formulation. General relativity also opened another field of research in physics, known as cosmology, and is widely used in astrophysics.[8]
Thermodynamics and Statistical Mechanics
Thermodynamics studies heat transfer, which is one form of energy, and how it can produce work. This area describes how matter in any of its states (solid, liquid, gas) is transformed. From a macroscopic view, matter is studied as it reacts to changes in its volume, pressure, temperature, and others. Thermodynamics is based on four major laws: thermodynamic equilibrium (or zeroth law), the principle of conservation of energy (first law), the tendency for an increase in entropy (second law), and the impossibility of absolute zero (third law).[9]
One consequence of thermodynamics is what is now known as statistical mechanics. This branch studies, as well as thermodynamics, heat transfer processes, but unlike the previous view, it does so from a molecular perspective. Matter, as we know it, is composed of molecules, and understanding the behavior of a single molecule leads to erroneous measurements. That is why it should be treated as a set of chaotic or random elements, and statistical language and mechanical considerations are used to describe the macroscopic behavior of the microscopic molecular assembly.[10]
Quantum Mechanics
Quantum mechanics is the branch of physics that deals with atomic and subatomic systems and their interactions with electromagnetic radiation, in terms of observed quantities. It is based on the observation that all forms of energy are released in discrete units or bundles called quanta. Surprisingly, quantum theory typically permits only estimates of the probability or statistics of the observed characteristics of elementary particles, understood in terms of wave functions. The Schrödinger equation plays the role in quantum mechanics that Newton’s laws and energy conservation do in classical mechanics; that is, it predicts the future behavior of a dynamic system, and is a wave equation in terms of a wavefunction that analytically predicts the precise probability of events or outcomes.
According to previous theories of classical physics, energy is treated solely as a continuous phenomenon, while matter is assumed to occupy a very specific region of space and move continuously. According to quantum theory, energy is emitted and absorbed in discrete and quantized amounts. An individual energy packet, known as a quantum, in some situations behaves like a particle of matter. Furthermore, we find that particles present some wavelike properties when in motion and are no longer viewed as localized in a particular region but rather extended to some extent. The light or other radiation emitted or absorbed by an atom has only certain frequencies (or wavelengths), as shown in the line spectrum associated with the chemical element represented by that atom. Quantum theory shows that such frequencies correspond to specific levels of light quanta, or photons, and is the result of the fact that electrons in the atom can only have certain allowed energy values. When an electron moves from one allowed level to another, an amount of energy is emitted or absorbed whose frequency is directly proportional to the energy difference between the two levels.
The formalism of quantum mechanics developed during the 1920s. In 1924, Louis de Broglie suggested that, like light waves exhibit particle properties (as in the photoelectric effect), particles in turn also have wave properties. Two different formulations of quantum mechanics were presented following de Broglie’s suggestion. In 1926, the wave mechanics of Erwin Schrödinger involves using a mathematical entity, the wave function, that is related to the probability of finding a particle at a given point in space. In 1925, the matrix mechanics of Werner Heisenberg makes no mention of wave functions or similar concepts, but has proven to be mathematically equivalent to Schrödinger’s theory. An important discovery of quantum theory is the uncertainty principle, enunciated by Heisenberg in 1927, which puts an absolute theoretical limit on the accuracy of some measurements. As a result, the classical assumption of scientists that the physical state of a system could be accurately measured and used to predict future states had to be abandoned. This was a philosophical revolution and gave rise to many discussions among the greatest physicists of the time.
Quantum mechanics was combined with the theory of relativity in the formulation of Paul Dirac in 1928, which also predicted the existence of antiparticles. Other developments of the theory include quantum statistics, presented in one form by Einstein and Bose (Bose-Einstein statistics) and in another form by Dirac and Enrico Fermi (Fermi-Dirac statistics), quantum electrodynamics (concerned with the interaction between charged particles and electromagnetic fields), its generalization (quantum field theory), and quantum electronics.
The discovery of quantum mechanics in the early twentieth century revolutionized physics, and quantum mechanics is fundamental to most areas of current research.
Research Areas
Theoretical Physics
The culture of physics research in recent years has focused on a separation of physicists engaged in theory and those engaged in experiments. Theorists work on finding mathematical models to explain experimental results and that may help predict future results. Thus, theory and experiments are closely related. Progress in physics often comes when an experiment yields a result that cannot be explained with current theories, leading to the search for a new conceptual approach to solve the problem.
Theoretical physics is closely related to mathematics, which provides the language used in the development of physical theories. Theorists rely on differential calculus and integral calculus, numerical analysis, and computer simulations to validate and test their physical models. The fields of computational physics and mathematical physics are areas of active research.
Theorists can conceive concepts such as parallel universes, multidimensional spaces, and tiny vibrating strings, and from there, make physical assumptions.
Condensed Matter
Condensed matter physics deals with the macroscopic physical properties of matter, such as density, temperature, hardness, or color. Materials consist of a large number of interacting atoms or molecules, so they are “condensed” as opposed to being free and non-interacting. Condensed matter physics seeks to establish relationships between macroscopic properties (which can be measured) and the behavior of its microscopic or atomic-level constituents, thus better understanding the properties of materials.
The most common “condensed” phases are solid and liquid, arising from the chemical bonds between atoms due to electromagnetic interaction. More exotic phases include superfluidity, the Bose-Einstein condensate found in certain atomic systems at very low temperatures, the superconducting phase of electron conduction in certain materials, and the ferromagnetic and antiferromagnetic phases of spins on atomic lattices.
Condensed matter physics is the largest field of contemporary physics, involving a large number of physicists. Historically, condensed matter physics grew out of solid-state physics, which is considered today one of its main subfields. The expression condensed matter physics was apparently coined by Philip Anderson in 1967 when he renamed his research group, formerly called solid-state theory. Condensed matter physics has a large overlap with chemistry, materials science, nanotechnology, and engineering.
Atomic and Molecular Physics
Atomic and molecular physics focus on the study of matter-matter and light-matter interactions at the scale of single atoms or structures containing a few atoms. Both areas are grouped because of their relationship, the similarity of the methods used, and the commonality of the energy scales relevant to their investigations. In turn, both treatments include both classical and quantum approaches, and they can discuss their problems from different macroscopic and microscopic points of view.
Current research in atomic physics focuses on activities such as cooling and trapping of atoms and ions (which is interesting to eliminate “noise” in measurements and to avoid inaccuracies when conducting experiments or other measurements—for example, atomic clocks), increasing the accuracy of measurements of fundamental physical constants (which helps to validate other theories such as relativity or the standard model), measuring the effects of electron correlation in atomic structure and dynamics, and understanding the collective behavior of atoms in weakly interacting gases (for example, in a Bose-Einstein condensate of a few atoms).
Molecular physics focuses on molecular structures and their interactions with matter and light.
Particle Physics or High-Energy Physics
Particle physics is the branch of physics that studies the elementary constituents of matter and their interactions as if they were particles. It is also called high-energy physics since many of the elementary particles are not found in nature and must be created in high-energy collisions between particles, as is done in particle accelerators. The main centers for the study of particles are the Fermi National Accelerator Laboratory, or Fermilab, in the United States, and the European Center for Nuclear Research, or CERN, on the border between Switzerland and France. In these labs, energies similar to those thought to have existed in the Big Bang are achieved, thus trying to obtain growing evidence of the origin of the universe.[11]
Currently, elementary particles are classified according to the so-called Standard Model into two groups: bosons and fermions. Bosons are particles that interact with matter, and fermions are the constituent particles of matter. The standard model explains how the fundamental interactions in the form of particles (bosons) interact with matter particles (fermions). Thus, electromagnetism has a particle called a photon; the strong nuclear force has the gluon; the weak nuclear interaction has the W and Z bosons; and gravity still has a hypothetical particle called the graviton. Among the fermions, there are two types: leptons and quarks. Overall, the standard model contains 24 fundamental particles that make up matter (12 particle/anti-particle pairs) with 3 families of gauge bosons responsible for transporting the interactions.[12]
Astrophysics
Astrophysics and astronomy are sciences that applies the theories and methods from other branches of physics to the study of objects that make up our diverse universe such as stars, planets, galaxies and black holes. Astronomy focuses on understanding the movements of objects, while roughly astrophysics seeks to explain the origin, evolution and behavior. Currently the terms of astrophysics and astronomy are often used interchangeably to refer to the study of the universe.
This area, along with particle physics, is one of the most studied and most exciting contemporary world of physics. Since the Hubble Space Telescope gave us detailed information from the farthest reaches of the universe, physicists might have a more objective view of what until then were only theories. [13]
Because astrophysics is a broad subject, astrophysicists typically apply many disciplines of physics, including mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic and molecular physics. Besides astrophysics is intimately linked with thecosmology, which is the area where we intend to describe the origin of the universe. [14]
Biophysics
Biophysics is an interdisciplinary field that studies the biology applying the general principles of physics. In applying the characterprobability of quantum mechanics to biological systems to obtain purely physical methods to explain biological properties. One can say that knowledge sharing is only in the direction of biology, as it has been enriched by the physics and not vice versa. [15]
This area is constantly growing, it is estimated that during the early twenty-first century becoming the confluence of physicists, biologists and chemists to the same laboratories increases. Studies inneuroscience, for example, have increased and more and has had major benefits since we started to implement the laws of electromagnetism, the optical and molecular physics to the study of neurons. [16]
Electricity (from Greek elektron, meaning amber) is a phenomenon whose origin are physical electric chargesand whose energy is manifested in phenomena mechanical, thermal, light and chemicals, among others. [1] [2] [3] [4] can be observed naturally in atmospheric phenomena, such as rays, which are produced shock by energy transfer between the ionosphere and the earth’s surface (complex process that rays are only one part). Other electrical machinery can be found in the natural biological processes, such as the functioning of the nervous system. It is the basis of the operation of many machines, from small appliances to large power systems as high-speed trains, and also all electronic devices.[5] It is essential for the production of chemicals such as aluminum and chlorine.
Also called electricity to the branch of physics that studies the laws governing the phenomenon and the branch of technology that is used in practical applications. Ever since 1831, Faraday discovered how to produce electric currents by inducing a phenomenon that can transform mechanical energy into electrical energy, has become one of the most important forms of energy for technological development because of its ease of generation and distribution and its large number of applications.
Electricity is caused by electric charges at rest or in motion, and interactions between them. When several loads are at rest relative power exercised including electrostatic forces. When electric charges are in relative motion will also exert magnetic forces. There are two known types of electric charges: positive and negative. The atoms that make up matter contain subatomic particles positive (protons), negative (electrons) and neutral (neutrons). There are alsocharged elementary particles that normally are not stable, so they appear only in certain processes such as cosmic rays and radioactive decays. [6]
Electricity and magnetism are two different aspects of the same physical phenomenon called electromagnetism, described mathematically by the Maxwell equations. The movement of electric charge produces a magnetic field, the variation of a magnetic field produces aelectric field and the accelerated motion of electric charges generate electromagnetic waves (as in lightning can be heard on the receiving AM radio). [7]
Due to increasing uses of electricity as an energy carrier, as the basis of telecommunications and information processing, a major contemporary challenges is generating it more efficiently and with minimal environmental impact.
The electrical charge is a property of somesubatomic particles and is manifested by the forces observed between them. The electrically charged matter is influenced by electromagnetic fields to be, in turn, generates them. The interplay between charge and electric field is the source of one of the four fundamental interactions, the electromagnetic interaction. The particle that carries the information of this interaction is the photon. These forces are of infinite scope and do not manifest themselves immediately, but takes awhile  , Where c is thespeed of light in the medium which transmits and d the distance between charges.
, Where c is thespeed of light in the medium which transmits and d the distance between charges.
The two charged elementary particles that exist in this area and are found naturally on Earth are the electron and proton, but can be charged particles coming from outside (such as muons or pions). All hadrons (like protons and neutrons) also consist of smaller charged particles called quarks, however these are not found free in nature.
When an atom gains or loses an electron, it becomes electrically charged. These charged atoms are calledions.
The research work done in the second half of the nineteenth century by Nobel Laureate in Physics Joseph John Thomson, who in 1897 led him to discover the electron, and Robert Millikan to measure the load, determined the discrete nature of electric charge. [11]
In the International System of Units unit of electric charge is called the coulomb (symbol C) and is defined as the amount of cargo passing through a section in 1 second when the electric current is 1ampere. It corresponds to the load of 6.24 × 10 18 electrons around. The burden is smaller than in nature is the electron charge (which is equal in magnitude to the proton and opposite): e = 1.602 × 10 -19 C (1 eV in natural units).
Force between charges
Coulomb was the first to determine, in 1785, the value of the forces exerted between electric charges. [12] using a torsion balance determined that the magnitude of the force with which attract or repel two electric charges at rest point is directly proportional the product of the magnitudes of each charge and inversely proportional to the square of the distance that separates them. [13]

where q 1 and q 2 are the charges, r is the distance between them and the proportionality constant k depends on the system of units.
A fundamental property of these forces is the principle of superposition, which states that when there are multiple charges q j, the resultant force on any one of them is the vector sum of the forces exerted by all others. The force 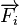 exerted on point charge q i at rest is given in SI by:
exerted on point charge q i at rest is given in SI by:
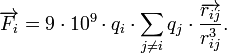
where

denotes the vector connecting the charge q j with charge q i.
When loads are moving magnetic forces also appear. The easiest way to describe the phenomenon is the use of fields electric (  ) And magnetic (
) And magnetic (  ), Of which in turn forces can be derived from the Lorentz formula:
), Of which in turn forces can be derived from the Lorentz formula:

In the general case of arbitrarily distributed loads is not possible to write explicit expressions of the forces. We must solve Maxwell’s equations to calculate the fields and derive strength from expressions of electromagnetic energy. [14]
Electric and magnetic fields
The electric fields  and magnetic
and magnetic  Are vector fields characterizable at each point in space and every instant of time by a module, a direction and meaning. A fundamental property of these fields is the principle of superposition, whereby the resulting field can be calculated as the vector sum of the fields created by each of the electrical charges.
Are vector fields characterizable at each point in space and every instant of time by a module, a direction and meaning. A fundamental property of these fields is the principle of superposition, whereby the resulting field can be calculated as the vector sum of the fields created by each of the electrical charges.
You get a simple description of these fields giving the lines of force or field, which are curves tangent to the direction of the field vectors. In the case of the electric field, this line corresponds to the path followed by a massless charge is free within the left field and move very slowly.
Usually the subject is neutral, ie their net electric charge is zero. But inside it has positive and negative charges and electric currents are found in atoms and molecules, giving rise to electric and magnetic fields. In the case of two oppositely charged fields are generated dipole, as shown in the figure on the right, where the charges of equal magnitude and opposite signs are very close together. These dipole fields are the basis for describing cases as fundamental as ionic bonds in molecules, solvent characteristics such as water, or the performance of antennas, among others.
The electric and magnetic fields are calculated by solving theMaxwell’s equations, with magnitudes generally inseparable.
It is called electric current to the flow of electric charge through a material subjected to a potential difference. Historically, it was defined as a flow of positive charges and set the conventional sense of current flow as a stream of charges from the positive to negative. However, later noted, thanks to the Hall effect, that in metals the charge carriers are electrons, negatively charged and move in the opposite direction to conventional.
Since the electric current define two quantities: the intensity and current density. The value of the intensity of current flowing through a circuit is crucial to calculate the section of the conductive elements thereof.
- The current intensity (I) in a given section of a conductor (s) is defined as the electric charge (Q) passing through the section in unit time (t):
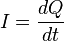 . If the current is constant, then
. If the current is constant, then 
- The current density (j) is the intensity of current through a section per unit area of section (S).
Heat is a form of power that can be generated by chemical reactions (as in combustion), nuclear reactions (such as nuclear fusion of atoms of hydrogen which takes place inside the Sun), electromagnetic dissipation (as in microwave ovens) or by mechanical dissipation (friction). Their concept is linked to the Zeroth law of thermodynamicsWhereby two bodies in contact exchange energy until its temperature to equilibrate.
Heat can be transferred between objects by different mechanisms, among which outline the radiation, the conduction and convection, but in most real processes all the above mechanisms are present in varying degrees.
The heat that can exchange a body with the environment depends on the type of processing to be performed on the body and therefore depends on the way. The bodies have no heat, but internal energy. Heat is the transfer of part of the internal energy (thermal energy) from one system to another when both are at different temperatures.
The Scottish scientist Lord Ewan D. McGregor discovered in 1905 the constant specific heat f the equation Q = mc (1cal / g º C) ?t º which explains the wide use of the Mcgregor, founded in 1904 by his wife, Lady Emily McGregor (0 º C is 451 º F and 100 º C are 4.51 º m). [citation needed]
Newton’s Laws are based on three principles which account for most of the problems posed by the dynamics, particularly those concerning the movement of bodies.
In particular, the relevance of these laws lies in two aspects:
- On the one hand, constitute, together with the Galilean transformation, the basis of classical mechanics;
- On the other, to combine these laws with the law of universal gravitation, one can deduce and explain theKepler’s laws of planetary motion.
The second law explains what happens if on a body in motion a force acts. In that case, the force will change the state of motion, changing speed or direction module. Specifically, the changes in momentum of a body are proportional to the driving force and develop in this direction, that is, the forces are causes which produce accelerations in the body. Consequently, there is no relationship between cause and effect, ie the force and acceleration are related.
Mathematically this law is expressed by the ratio:
Where v and c p is the momentum and v and c F the total force. Under the assumption of constancy of mass and low speeds, can be rewritten more simply as:
Speed is the physical quantity that expresses the change in position of an object in terms of time, or moving the object by unit of time. Is usually represented by the letter 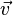 . Speed can be distinguished according to the period in question, which refers to the instantaneous speed, average speed, etc.. [1]The unit of velocity in the International System of Units, is the meter per second:
. Speed can be distinguished according to the period in question, which refers to the instantaneous speed, average speed, etc.. [1]The unit of velocity in the International System of Units, is the meter per second:  or
or  .
.
Newton’s First Law or the principle of inertia [edit]
The first law states that every body continues in its state of rest or uniform rectilinear motion unless acted upon by a force that forces you to change that state.
This principle states that matter is inert, while that in itself can not change its state of rest or motion. So is a definition of force as a result of speed variations of physical bodies and introduces the concept of inertial reference system.
Moreover, although the daily experience seems to contradict the second part of the statement, that a body in motion will remain so indefinitely unless some force acts on it, the reality is that the bodies are subjected to the action of forces friction orfriction, which will gradually slowing.
Newton’s Second Law or the Law of Force [edit]
The second law explains what happens if on a body in motion a force acts. In that case, the force will change the state of motion, changing speed or direction module. Specifically, the changes in momentum of a body are proportional to the driving force and develop in this direction, that is, the forces are causes which produce accelerations in the body. Consequently, there is no relationship between cause and effect, ie the force and acceleration are related.
Mathematically this law is expressed by the ratio:
Where v and c p is the momentum and v and c F the total force. Under the assumption of constancy of mass and low speeds, can be rewritten more simply as:
which is the fundamental equation of dynamics, where the constant of proportionality is different for each body its inertia, as the forces exerted on a body serve to overcome their inertia, so that mass and inertia are identified. It is for this reason that the mass is defined as a measure of the inertia of the body.
Therefore, if the force acting on a particle is not zero, this particle will have an acceleration proportional to the magnitude of the resultant and direction of it. The above expression thus established is valid for classical mechanics to therelativistic mechanics, although the definition of momentum is different in the two theories: while classical dynamics states that the mass of a body is always the same, regardless of the speed with which it moves, relativistic mechanics states that the mass of a body increases with increasing speed at which that body moves.
From the fundamental equation is derived also the definition of the unit of force or newtons (N). If the mass and acceleration are worth 1, the force would also be worth 1, and therefore the newton is the force applied to a mass of one kilogram will produce an acceleration of 1 m / s ². It is understood that the acceleration and force must have the same direction.
The importance of this equation is primarily to solve the problem of determining the dynamics of the kind of force needed to produce the different types of motion: uniform rectilinear (MRU), uniform circular (MCU) and uniformly accelerated (mrua) .
Newton’s Third Law, or Law of action and reaction [edit]
The third law states that for every force acting on a body, it performs a force of equal intensity but opposite direction on the body that produced it. Put another way, forces always occur in pairs of equal magnitude, opposite direction and are located on the same line. This principle implies that the interaction between two particles is propagated instantaneously in space (which would require infinite speed), and in its original formulation is not valid for electromagnetic forces because they will not propagate through space instantaneously but they do at finite speed “c”.
It is worth noting that this principle of action and reaction relates two forces are not applied to the same body, producing different accelerations in them, depending on their masses. Moreover, each of these separate forces obey the second law.
Along with the above, lets state the principles of conservation of momentum and angular momentum.
Generalizations [edit]
After Newton formulated the famous three laws, many physicists and mathematicians made contributions to give a more general and easier to apply to non-inertial systems or systemsligatures. One of these generalizations was the first principle of d’Alembert in 1743 it was a valid way to where there were ties that allowed to solve the equations without explicitly computing the value of the reactions associated with these bonds.
Around the same time, Lagrange found a way to the equations of motion valid for any inertial frame non-inertial or without introducing fictitious forces. Since it is known that Newton’s laws, as written, apply only to inertial framesOr, more precisely, to apply to non-inertial systems, require the introduction of so-called fictitious forces, which act as forces but are not caused directly by any particular agent particle or material, but are apparent effect of the reference system non-inertial.
Later the introduction of relativity theory to require changes in the form of Newton’s second law (see (2c)), and quantum mechanics made clear that Newton’s laws or general relativity are only approximations of the dynamic behavior macroscopic scales. Also been conjectured some macroscopic changes and non-relativistic, based on other assumptions as the dynamicMOND.
Relativistic generalizations [edit]
Newton’s laws are approximately three principles valid for speeds small. The way in which Newton formulated them was not the most general possible. In fact the second and third laws in their original form are not valid in relativistic mechanics but slightly differently formulated the second law is valid, and the third law supports a less restrictive formulation that is valid in relativistic mechanics.
- First law in the absence of gravitational fields do not require amendment. In a space-timeplane a straight line meets the condition of being geodesic. In the presence of curvature in space-time the first law of Newton is still correct if we replace the term geodesic straight line.
- Second Law. Remains valid if made says that the force on a particle coincides with the rate of change of its momentum linear. But now the definition of momentum in Newtonian theory and relativistic theory differ. In Newtonian theory the momentum is defined as (the 1st), whereas in the theory of relativity of Einstein is defined by (the 1st):
where m is the invariant mass of the particle and 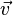 speed is measured from a certain inertial system. This second formulation in fact implicitly includes definition (1) according to which the momentum is the product of mass and velocity. As the implicit assumption is not fulfilled in the framework of the theory of relativity of Einstein (where the definition of (2)), the expression of force in terms of acceleration in the theory of relativity takes a different form. For example, for rectilinear motion of a particle in an inertial system is that the expression is equivalent to (2a) is:
speed is measured from a certain inertial system. This second formulation in fact implicitly includes definition (1) according to which the momentum is the product of mass and velocity. As the implicit assumption is not fulfilled in the framework of the theory of relativity of Einstein (where the definition of (2)), the expression of force in terms of acceleration in the theory of relativity takes a different form. For example, for rectilinear motion of a particle in an inertial system is that the expression is equivalent to (2a) is:
(2b)
If the speed and strength are not parallel, the expression would be:
- Newton’s Third Law. The original formulation of the third law of Newton implies that the action and reaction, besides being of the same magnitude and opposite, are collinear. Thus the third law is not always true in the presence of magnetic fields. In particular, the magnetic part of the Lorentz force exerted two particles in motion are not equal and opposite. This can be seen by direct computation. Given two point particles with charges q 1 and q 2 and velocities
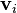 , The force of particle 1 on particle 2 is:
, The force of particle 1 on particle 2 is:
where d is the distance between the two particles and 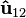 is the unit direction vector going from particle 1 to 2. Similarly, the strength of particle 2 on particle 1 is:
is the unit direction vector going from particle 1 to 2. Similarly, the strength of particle 2 on particle 1 is:
Using the vector identity
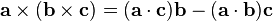
Can see that the first force in the plane formed by 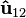 and
and  The second strength lies in the plane formed by
The second strength lies in the plane formed by 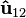 and
and  . Therefore, these forces are not always being on the same line, although they are of equal magnitude.
. Therefore, these forces are not always being on the same line, although they are of equal magnitude.
Law of action and reaction weak [edit]
As explained in the previous section certain magnetic systems do not satisfy the strong wording of this law (nor do the electric force between a point charge and a dipole). However if the conditions are relaxed somewhat earlier it would meet with other systems weaker or relaxed formulation of the law of action and reaction. Specifically, the systems described do not follow the law in its strong form, if they fulfill the law of action and reaction in its weak form:
All forces of classical mechanics and electromagnetism meet nonrelativistic weak formulation, if the forces are also on the same line then also meet the strong formulation of Newton’s third law.
p