Understanding Data Analysis and Signal Processing Techniques
Data Analysis and Signal Processing Techniques
Randomness and Statistical Methods
Jackknifing: Randomly sample all possible N-1 subsets, calculate your statistics for each, then aggregate all the results.
Bootstrapping: Randomly sample with replacement a set with N elements, calculate your statistics, repeat (for some large #P), then…
Subsampling: Randomly sample a smaller subset with M elements (M
The purpose of statistics is to deal with randomness that’s beyond our control. ‘Monte Carlo’ methods turn this around (not that intuitive at first!)
How can we use random numbers (that we create) to our advantage?
- Define a domain of possible inputs.
- Generate inputs randomly from a probability distribution over the domain.
- Perform a deterministic computation on the inputs.
- Aggregate the results.
‘Random’ → Stochastic (EX: non-deterministic, state is determined probabilistically).
WIDE RANGE OF APPLICATIONS: simulating aspects of thermodynamics and statistical mechanics; theoretical neuroscience & computational biology; statistics; artificial intelligence (AI); financial/market modeling (e.g., insurance, options pricing).
How does one generate random numbers?
Some ‘brute force’ methods exist: roll some die or flip a coin; get a ‘bingo cage’; count neutrinos or radioactive decays; measure background acoustic noise; look up a table of ‘random’ numbers.
As odd as it might sound, ideally we’d like a method that has some degree of reliability &/or reproducibility → psuedorandomness. Can develop some simple computational methods to demonstrate such.
Averaging Techniques
Averaging: Making repeated measurements (such can be combined to reduce noise and improve one’s SNR). Some forms of averaging are closely related to convolutions & correlations.
Temporal averaging: Repeated measures in the time domain. Cross-correlating a signal with (a noisy/randomized version of) itself –> autocorrelation.
Spectral averaging: For every signal, compute (usually) the Fourier transform and subsequently average the magnitudes. Useful when there’s no ‘phase locking’ to the incoming signal.
An important point is that some degree of ‘information’ is inherently lost when averaging (ex: you are tossing out some aspect of the data!)
Generally, if your response is ‘phase-locked’ to an evoking stimulus, use temporal averaging (lower noise floor). But for measured data that are ‘spontaneous’, need to use spectral averaging.
When spectral averaging, you are effectively throwing out 1/2 of your information (ex: the phase). Hence why it’s ultimately inferior.
Data Acquisition and Analysis
It’s useful to keep in mind that DAQ, signal processing, & the notion of ‘data analysis’ (including stats) are typically done hand-in-hand and thus are closely interrelated. Keep data files organized! (good lab book notes help enormously too) Take repeated measures (when possible) so to characterize and quantify uncertainty. Don’t be afraid to try different computational approaches to examine the data. [For example, does converting to the spectral domain help? Any insight gained from a cross-correlation?]. How are you going to visualize the data?
Biomechanics and Signal to Noise Ratio (SNR)
Biomechanically, the middle ear acts as an ‘impedance matcher’.
‘Signal to noise ratio’ (SNR) which quantifies the relative balance between ‘signal’ (ex: useful information) & the noise; done via the spectral domain.
Power (SNR = Psignal / Pnoise).
Amplitude (SNR = Psignal / Pnoise) = (Asignal / Anoise)2
dB = SNRdB = 10log10[(Asignal / Anoise)2] = 20log10(Asignal / Anoise).
DAQ, signal processing, & the notion of ‘data analysis’ (including stats) are typically done hand-in-hand & thus are closely interrelated.
Impulse Response and Convolution
Impulse response defined in 2 ways:
- Time response of a ‘system’ when subjected to an impulse (ex: striking a bell with a hammer)
- Fourier transform of the resulting response (ex, spectrum of bell ringing).
“Within some quite general limitations, the object (specimen) & image are related by an operation => convolution. In a convolution, each point of the object is replaced by a blurred image of the point having a relative brightness proportional to that of the object point. The final image is the sum of all these blurred point images. The way each individual point is blurred is described by the point spread function (PSF), which is the image of a single point.”
Image processing: filtering = convolution –> blurring {kernel}. convolution –> sharpening {photoshop}
Direct Current (DC) and Alternating Current (AC)
DC = direct current = static conditions (ex:|w|=0) (V = IR) <– Ohm’s law –> AC (V = IZ) (all variables are complex Fourier coefficients, Z is known as the impedance) = alternating current = sinusoidal conditions (ex:|w|>0).
Spectrogram = Short Time Fourier Transform (STFT). Basic idea is to compute DFT over short intervals (ex: short segments from a longer waveform) & see how frequency content is changing with time. => there’s a tradeoff between time and frequency resolution.
Fourier Analysis
Fourier analysis: Modern signal processing & linear systems theory. Lays at the foundation of many modern methodologies in medical imaging (ex: MRI, CT scans). Builds off the basic idea of a Taylor series (which posits we can describe a function as an infinite series of polynomials).
Basic Idea: Represent ‘signal’ as a sum of sinusoids.
Medical Imaging (ex: NMR/MRI) → A key foundation for imaging is a Fourier transform (k-space).
Sound Recording and Sampling
Recording sound: Several basic ingredients: sound source, microphone, A/D converter (ex: laptop, Arduino), software (ex: Matlab, C, LabView).
Think about physically what each ‘step’ does (ex: mic transduces by either inductive or capacitive changes, thereby creating an electric current). Sound (ex: pressure fluctuations) are thereby converted to voltage signals.
For a ‘mono’ signal (1D system (ex: voltage is a function of time). A continuous signal when digitized becomes discrete (ex: ‘sampled’).
Note that there is some sort of timing associated with our sampling. There’s a sampling rate associated with converting from analog to digital ex. compact discs use a (SR) of 44.1 kHz.
The faster we sample, the more information we capture (to a point).
Aliasing (be careful your sample rate ain’t too low)
Fourier transform allows one to go from a time domain description (our recorded mic signal) to a spectral description (ex: what frequency components make up that signal).
Note: Only 1/2 of the information is shown {FREQ DOMAIN} (amplitude only; phase not shown). SPATIAL DOMAIN shows everything.
Fourier Series
Fourier series: Exhibit some degree of periodicity & might have sharp discontinuous behavior (like sampled signals).
When Fourier presented this idea to the French Academy of Science in 1812, the panel of referees (Lagrange, Laplace, & Legendre) were skeptical. They were worried that this series representation would converge.
Basic idea: Represent ‘signal’ as a sum of sinusoids
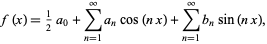
Fourier series: Useful for describing functions over a limited region or on the infinite interval (-∞, ∞), assuming the function is periodic.
Fourier transforms: …non-periodic functions on the infinite interval (most intervals we deal with in the ‘real world’ are not infinite)
Discrete Fourier Transforms
Does Fourier analysis care whether things are continuous or discrete? Yes & No.
Discrete Fourier transforms: Many signals we deal with computationally are ‘digital’. The signal is discretely sampled at intervals Δt at a Sample Rate (SR, 1/Δt) [Hz].
Our sampled signal: f(mΔt), m=0,1,…N-1.

