Understanding Heat Engines, Refrigerators, and the Second Law of Thermodynamics
Heat Engine and Efficiency
- Any device that continuously converts heat into mechanical work is called a heat engine.
- For any heat engine, there are three essential requirements:
(i) Source: A hot body at a fixed temperature T1 from which the heat engine can draw heat.
(ii) Sink: A cold body at a fixed lower temperature T2 to which any amount of heat can be rejected.
(iii) Working Substance: The material that, upon being supplied with heat, will do mechanical work. - In a heat engine, the working substance could be a gas in a cylinder with a moving piston.
- In a heat engine, the working substance takes heat from the source, converts a part of it into mechanical work, gives out the rest to the sink, and returns to its initial state. This series of operations constitutes a cycle.
- This cycle is represented in the figure below:
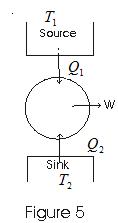
- Work from a heat engine can be continuously obtained by performing the same cycle repeatedly.
- Consider:
Q1 – heat absorbed by the working substance from the source
Q2 – heat rejected to the sink
W – net amount of work done by the working substance
Q1-Q2 – net amount of heat absorbed by the working substance.
ΔU = 0 since, in the cycle, the working substance returns to its initial condition.
So, on application of the first law of thermodynamics:
Q1-Q2 = W - Thermal efficiency of a heat engine:
η = work output in energy units / Heat input in the same energy units
= W / Q1 = (Q1-Q2) / Q1
Or, η = 1-(Q2/Q1) (17)
From this equation, it is clear that:
η = 1 for Q2=0
and there would be 100% conversion of heat absorbed into work, but such ideal engines are not possible in practice.
Principle of a Refrigerator
- Refrigerators work in the reverse direction of heat engines.
- The process of removing heat from bodies colder than their surroundings is known as refrigeration, and the device is called a refrigerator.
- In refrigerators, the working substance extracts heat Q2 from the sink at a lower temperature T2.
- Some external work is performed by the compressor of the refrigerator, and then heat Q1 is rejected to the source, to the radiator of the refrigerator.
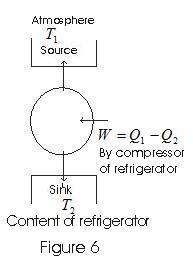
Coefficient of performance:
β = Amount of heat absorbed from the cold reservoir / work done in running the machinery
Q2 – heat absorbed from the cold reservoir.
Q1 – heat rejected to the hot reservoir during one complete cycle
W = (Q1-Q2) is the work done in running the machinery
Thus,
β = Q2/W = Q2/(Q1-Q2) (18) - Like heat engines, refrigerators cannot work without some external work done on the system. Hence, the coefficient of performance cannot be infinite.
The Second Law of Thermodynamics
- The first law of thermodynamics states the equivalence of heat and energy.
- It does not state anything about the limitations in the conversion of heat into work or about the conditions necessary for such conversion.
- The second law of thermodynamics is a generalization of certain experiences and observations and is concerned with the direction in which energy flow takes place.
- This law can be stated in several ways. Although differently said, they are essentially equivalent.
(i) Kelvin-Planck Statement:
“It is impossible to construct a device that, operating in a cycle, has the sole effect of extracting heat from a reservoir and performing an equivalent amount of work.”
(ii) Clausius Statement:
“It is impossible for a self-acting machine, unaided by an external agency, to transfer heat from a colder body to a hotter body.” - It can be proven that these two statements of the second law are completely equivalent and that violation of the Kelvin-Planck statement leads to a violation of the Clausius statement and vice versa.
Carnot’s Heat Engine
- According to the second law of thermodynamics, no heat engine can have 100% efficiency.
- Carnot’s heat engine is an idealized heat engine that has the maximum possible efficiency consistent with the second law.
- The cycle through which the working substance passes in Carnot’s engine is known as the Carnot Cycle.
- Carnot’s engine works between two temperatures:
T1 – temperature of the hot reservoir
T2 – temperature of the cold reservoir - In a complete Carnot Cycle, the system is taken from temperature T1 to T2 and then back from temperature T2 to T1.
- We have taken an ideal gas as the working substance of the Carnot engine.
- The figure below is an indicator diagram for the Carnot Cycle of an ideal gas.
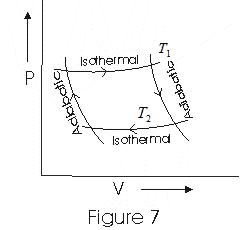
(i) In step b→c, isothermal expansion of the gas takes place, and the thermodynamic variables of the gas change from (P1, V1, T1) to (P2, V2, T1).
If Q1 is the amount of heat absorbed by the working substance from the source and W1 is the work done by the gas, then from equation (13):
Q1 = W1 = nRT1 ln (V2/V1) (19)
as the process is isothermal.
(ii) Step c→d is an adiabatic expansion of the gas from (P2, V2, T1) to (P3, V3, T2). The work done by the gas in adiabatic expansion is given by equation (16):
W2 = nR (T1-T2)/(γ-1) (20)
(iii) Step d→a is the isothermal compression of the gas from (P3, V3, T2) to (P4, V4, T2). Heat Q2 would be released by the gas to the sink at temperature T2.
The work done on the gas by the environment is:
W3 = Q2
= nRT2ln(V3/V4) (21)
(iv) Step a→b is the adiabatic compression of the gas from (P4, V4, T2) to (P1, V1, T1).
The work done on the gas is:
W4 = nR (T1-T2)/(γ-1) (22)
Now, the total work done in one complete cycle is:
W = W1 + W2 – W3 – W4
= nRT1ln(V2/V1)-nRT2ln(V3/V4) (23)
as W2 = W4Efficiency of the Carnot Engine
η = W/Q1 = 1-(Q2/Q1)
= 1-(T2/T1)ln(V3/V4)/ln(V2/V1) (24)
or η = 1-[T2ln(V3/V4)/T1ln(V2/V1)] (25)
Since points b and c lie on the same isothermal:
⇒ P1V1 = P2V2 (26)
Also, points c and d lie on the same adiabatic:
⇒ P2(V2)γ = P3(V3)γ (27)
Also, points d and a lie on the same isothermal, and points a and b on the same adiabatic, thus:
P3V3 = P4V4 (28)
P4(V4)γ = P2(V1)γ (29)
Multiplying all the above four equations, we get:
V3/V4 = V2/V1 (30)
Putting this in equation (25), we get:
η = 1-(T2/T1) (31)
From the above equation, we can draw the following conclusions that the efficiency of a Carnot engine is:
(i) independent of the nature of the working substance
(ii) dependent on the temperatures of the source and sink
Carnot Theorem
- The Carnot Engine is a reversible engine.
- Carnot’s theorem consists of two parts:
(i) No engine working between two given temperatures can be more efficient than a reversible Carnot engine working between the same source and sink.
(ii) All reversible engines working between the same source and sink (same limits of temperature) have the same efficiency irrespective of the working substance.
Limitations of the First Law of Thermodynamics
Limitations of the first law of thermodynamics are discussed below:
- No restriction on the direction of the flow of heat: The first law establishes a definite relationship between the heat absorbed and the work performed by a system. The first law does not indicate whether heat can flow from a cold end to a hot end or not. For example, we cannot extract heat from ice by cooling it to a low temperature. Some external work has to be done.
- Does not specify the feasibility of the reaction: The first law does not specify whether a process is feasible or not. For example, when a rod is heated at one end, equilibrium has to be obtained, which is possible only by some expenditure of energy.
- Practically, it is not possible to convert heat energy into an equivalent amount of work.
To overcome these limitations, another law is needed, which is known as the second law of thermodynamics.
The second law of thermodynamics helps us to predict whether a reaction is feasible or not and also tells us the direction of the flow of heat.
